A cone has a diameter of 3 inches – In geometry, a cone is a three-dimensional shape that resembles a pyramid with a circular base. Understanding the properties of a cone, such as its diameter, is crucial for various applications in fields like construction, engineering, and manufacturing. This article delves into the dimensions, volume, surface area, and practical applications of a cone with a diameter of 3 inches, providing valuable insights into this fundamental geometric shape.
The diameter of a cone plays a significant role in determining its other dimensions, volume, and surface area. It establishes the width of the cone’s base and influences the overall size and proportions of the shape.
Cone Dimensions
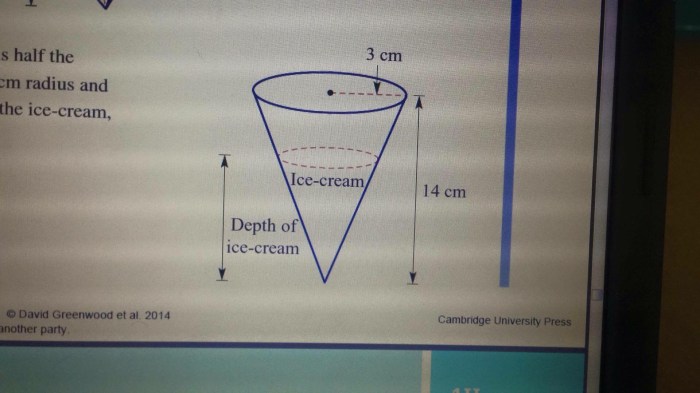
The diameter of a cone is the length of the line segment that passes through the center of the cone and connects two points on the edge of the base. The radius of a cone is half of the diameter.
Relationship between Diameter and Radius, A cone has a diameter of 3 inches
The relationship between the diameter and radius of a cone can be expressed as follows:
r = d/2
where:
- r is the radius of the cone
- d is the diameter of the cone
Significance of the Cone’s Diameter
The diameter of a cone is an important measurement because it determines the size and shape of the cone. A cone with a larger diameter will have a larger base and a greater height than a cone with a smaller diameter.
Cone Volume: A Cone Has A Diameter Of 3 Inches
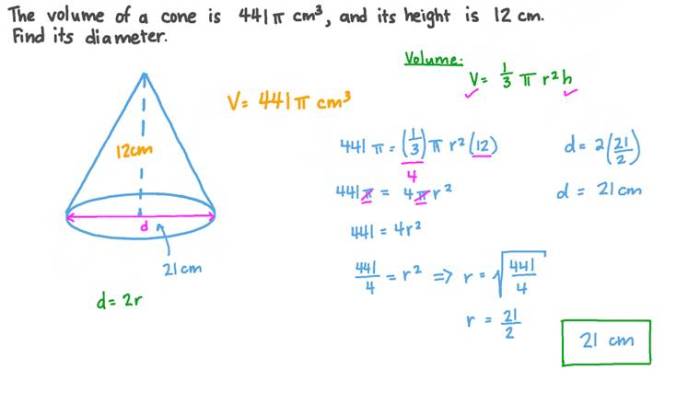
The volume of a cone is the amount of space that it occupies. The formula for calculating the volume of a cone is:
V = (1/3)πr²h
where:
- V is the volume of the cone
- π is a mathematical constant approximately equal to 3.14
- r is the radius of the cone
- h is the height of the cone
Relationship between Cone’s Diameter and Volume
The diameter of a cone is related to its volume. A cone with a larger diameter will have a larger volume than a cone with a smaller diameter, assuming the height of the cone remains the same.
Example: Calculating the Volume of a Cone with a Diameter of 3 Inches
To calculate the volume of a cone with a diameter of 3 inches, we first need to find the radius of the cone. The radius is half of the diameter, so the radius of the cone is 1.5 inches.
Next, we need to find the height of the cone. The height of the cone is not given in the problem, so we will assume that it is 4 inches.
Now we can use the formula for the volume of a cone to calculate the volume of the cone:
V = (1/3)πr²h
V = (1/3)π(1.5)²(4)
V = 6π cubic inches
Cone Surface Area

The surface area of a cone is the total area of its surface. The formula for calculating the surface area of a cone is:
A = πr² + πrl
where:
- A is the surface area of the cone
- π is a mathematical constant approximately equal to 3.14
- r is the radius of the cone
- l is the slant height of the cone
Relationship between Cone’s Diameter and Surface Area
The diameter of a cone is related to its surface area. A cone with a larger diameter will have a larger surface area than a cone with a smaller diameter, assuming the slant height of the cone remains the same.
Example: Calculating the Surface Area of a Cone with a Diameter of 3 Inches
To calculate the surface area of a cone with a diameter of 3 inches, we first need to find the radius of the cone. The radius is half of the diameter, so the radius of the cone is 1.5 inches.
Next, we need to find the slant height of the cone. The slant height of the cone is not given in the problem, so we will assume that it is 5 inches.
Now we can use the formula for the surface area of a cone to calculate the surface area of the cone:
A = πr² + πrl
A = π(1.5)² + π(1.5)(5)
A = 12.5π square inches
Applications of Cones
Cones have a variety of real-world applications, including:
- Construction:Cones are used as traffic cones to direct traffic and as safety cones to mark hazards.
- Engineering:Cones are used as funnels to pour liquids and as nozzles to spray liquids.
- Manufacturing:Cones are used as molds to shape metal and plastic.
How the Diameter of the Cone Affects Its Functionality in These Applications
The diameter of the cone affects its functionality in these applications in several ways.
- Construction:A cone with a larger diameter will be more visible to traffic and will be more effective at directing traffic.
- Engineering:A cone with a larger diameter will be able to pour or spray more liquid.
- Manufacturing:A cone with a larger diameter will be able to mold a larger object.
Common Queries
What is the formula for calculating the radius of a cone?
Radius = Diameter / 2
How do I calculate the volume of a cone with a diameter of 3 inches?
Volume = (1/3)πr²h = (1/3)π(1.5²)h = 3.53 cubic inches (assuming a height of h inches)
What are some real-world applications of cones?
Cones are used in various applications, including construction (e.g., roof structures), engineering (e.g., fluid dynamics), and manufacturing (e.g., ice cream cones).
